When analyzing music, each diatonic triad is identified by a Roman numeral.

Four different types of roman numerals exist - one for each triad type.

Let's apply roman numerals to the C major scale.

Since the first triad is major, its roman numeral is upper-case.

The second and third triads are minor; therefore, their numerals are lower-case.
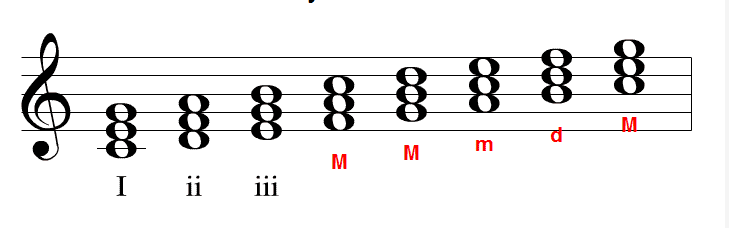
The fourth and fifth triads are major; therefore, their numerals are upper-case.

The sixth triad is minor, making its numeral lower-case.

Since the seventh triad is diminished, its roman numeral is lower-case and a little circle is added.

Finally, the last triad is a repeat of the first.

Next, we will apply roman numerals to the C natural minor scale.

Since the first triad is minor, its roman numeral is lower case.

The second triad is diminished; thus, we will use a lower-case numeral with the little circle.

Since the third triad is major, its numeral is upper-case.

The fourth and fifth triads are minor; therefore, their numerals are lower-case.

The sixth and seventh triads are major; therefore, their numerals are upper-case.

Again, the last triad is a repeat of the first.

Finally, we will apply roman numerals to the C harmonic minor scale.

Since the third triad is now augmented, its roman numeral is upper-case with an added plus sign.

The fifth triad is now major - making its numeral upper-case.

The seventh triad is now diminished - making its numeral lower-case with the little circle.

The roman numeral system can also be used to indicate inversions.

First inversion is represented by a small 6 after the roman numeral. This is due to the root being a generic sixth above the bass note.

Second inversion is represented with both a small 6 and 4. This is due to the root and third being a generic sixth and fourth above the bass note.

The fifth triad's numeral is also lower-case.























